Dynamic Soaring (DS)
Dave Reese's license plate says it all!

My first experience with dynamic soaring occurred in the fall of 1999. Pat Bowman showed me the technique at Parker Mountain one day and I have been hooked ever since. The speed and sounds coming from a sailplane flying well into the 100-200 mph range is a total adrenaline rush!
So what is dynamic soaring (DS)? DS differs from conventional soaring in that it doesn't use rising air to sustain flight. Energy is extracted from the air by flying in and out of airmasses moving at different speeds. DS is not new by any means as the Royal Albatross uses dynamic soaring as it flies over the ocean. It is done using the different wind speeds that occur as a result of the wind gradient that occurs over the ocean. See http://www.wfu.edu/albatross/atwork/dynamic_soaring.htm for a nice detailed example. DS at Parker Mountain (or anywhere for that matter) is different from the Albatross in that the space between the two different airmasses is much closer to each other and the contrasting airspeeds are much greater. As you will see in my diagram, instead of using wind gradient to establish different wind speeds, we use a sharp peaked mountain that causes the air to separate on the backside.
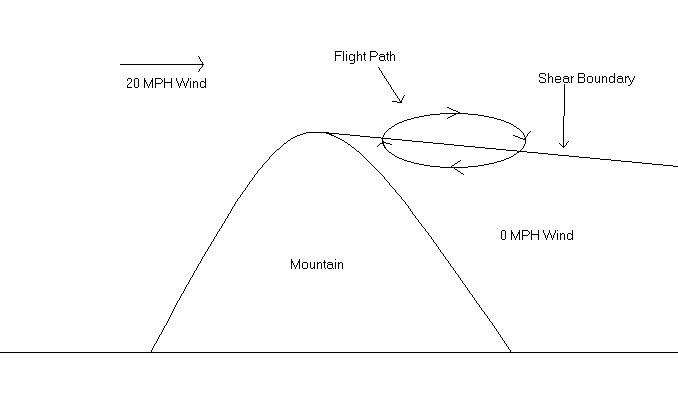
From a technical standpoint, I will refer to Joe Wurts' article in SE Modeler written in late 1998. He writes:
"One can derive the ratio of final velocity to initial velocity for a given rate of turn and a given turn L/D. It turns out that the wing loading drops out of the equations. The equation for final velocity divided by the initial velocity is:
V1/V0 = e^ (-theta/LD)
where,
V1 = final velocity
V0 = initial velocity
e = 2.7182818 (natural log #)
theta = turn angle, in radians (180 degrees = 3.14 radians)
L/D = Lift/Drag (glide ratio)
Armed with this equation, one can start to figure out the potential from dynamic soaring. Assume a delta wind velocity of 30 mph, and an L/D of 25 (good for a model sailplane). So, the airplane heading downwind has a ground speed of 60 mph (30 mph from airspeed plus the 30 mph tailwind). After crossing the shear boundary, the airspeed becomes equal to the ground speed. Therefore, the plane is flying 60 mph ground speed in the "dead air" on the backside of the hill. Now, do a 180 degree turn in the dead air. The velocity ratio, V1/V0, for a 180 degree turn is 0.8819. Therefore, the airspeed and ground speed after the turn is 52.9 mph. Now, cross the shear boundary again into the headwind, and the airspeed is now 82.9 mph. Do another 180 degree turn, and the airspeed is 73.1 mph. In a single 360 degree turn, the sailplane gained 43 mph! Eventually, if you keep doing these turns, the velocity loss from the turn will equal the velocity gain from crossing the shear boundary. But, the final velocity will be about 224 mph!
An interesting note is that the maximum potential final velocity is linearly dependent on the velocity delta across the shear boundary. So if the shear delta goes from 30 to 60 mph, the final velocity potential goes from 224 mph to 448 mph!"
In October of 1999, I watched Joe blow up two strong composite ships in one day flying in about 45-50 mph winds. He was only able to make 2 1/2 turns with each ship before the g-load in the turns caused the wings to fail. The first plane broke the solid carbon joiner that connects the wings to the fuselage. The second wing failed in the wing panel itself. It rained fiberglass confetti for at least another 45 seconds after the failure. The speed and acceleration was incredible! Since then I have managed to break 3 sailplanes in flight as a result of structural failure while dynamic soaring.
It has to be seen AND heard to be appreciated. I think it is fascinating.
I